Выполните следующие задания. Ответы (и при необходимости решение) присылать мне на почту (glushhenko.vv@school362.ru). Способ решения выбираете самостоятельно.
Задание 1. Ниже на четырёх языках записан алгоритм. Получив на вход число x, этот алгоритм печатает два числа: a и b. Укажите наименьшее из таких чисел x, при вводе которых алгоритм печатает сначала 2, а потом 63.
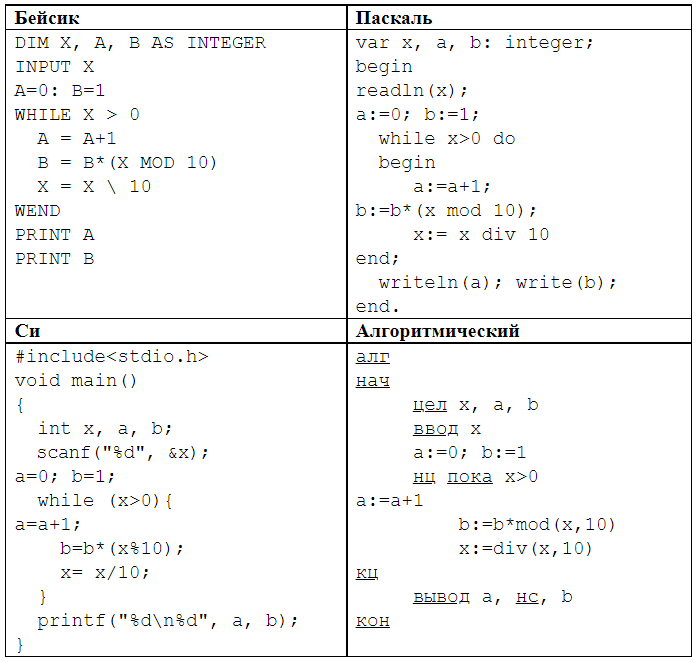
Задание 2. Ниже на четырёх языках программирования записан алгоритм. Получив на вход число x, этот алгоритм печатает два числа: a и b. Укажите наибольшее из таких чисел x, при вводе которых алгоритм печатает сначала 2, а потом 11.

Задание 3. Ниже на четырёх языках записан алгоритм. Получив на вход число x, этот алгоритм печатает два числа: a и b. Укажите наименьшее из таких чисел x, при вводе которых алгоритм печатает сначала 15, а потом 6.

Алгоритм преобразует его по следующим правилам.
1.В конец числа (справа) дописывается 1, если количество единиц в его записи нечётно. В противном случае, если количество единиц чётно, дописывается 0. Например, число 11100 преобразуется в число 111001.
2.Та же операция применяется к полученному 6-значному двоичному числу.
3.Полученное двоичное число переводится в десятичную систему счисления.
Укажите десятичное число, которое может быть результатом работы алгоритма.
Если таких чисел несколько, укажите меньшее из них.
Ответ:
54
152
91
116
Задание 5. Исполнитель КУЗНЕЧИК живёт на числовой оси. Начальное положение КУЗНЕЧИКА – точка 0. Система команд Кузнечика:
Вперед 6 – Кузнечик прыгает вперёд на 6 единиц,
Назад 4 – Кузнечик прыгает назад на 4 единицы.
Какое наименьшее количество раз должна встретиться в программе команда «Назад 4», чтобы Кузнечик оказался в точке 28?
Задание 6. Алгоритм получает на вход натуральное число N > 1 и строит по нему новое число R следующим образом:
1. Если исходное число кратно 2, оно делится на 2, в противном случае из него вычитается 1.
2. Если полученное на предыдущем шаге число кратно 3, оно делится на 3, в противном случае из него вычитается 1.
3. Если полученное на предыдущем шаге число кратно 7, оно делится на 7, в противном случае из него вычитается 1.
4. Число, полученное на шаге 3, считается результатом работы алгоритма.
Пример. Дано число N = 44. Алгоритм работает следующим образом:
1. Число 44 кратно 2, оно делится на 2, получается 22.
2. Число 22 не кратно 3, из него вычитается 1, получается 21.
3. Число 21 кратно 7, оно делится на 7, получается 3.
4. Результат работы алгоритма R = 3.
Сколько существует различных натуральных чисел N, при обработке которых получится R = 1?
Задание 7. Алгоритм получает на вход натуральное число N > 1 и строит по нему новое число R следующим образом:
1. Вычисляется сумма чётных цифр в десятичной записи числа N. Если чётных цифр в записи нет, сумма считается равной нулю.
2. Вычисляется сумма цифр, стоящих на чётных местах в десятичной записи числа N без ведущих нулей. Места отсчитываются слева направо (от старших разрядов к младшим, начиная с единицы). Если число однозначное (цифр на чётных местах нет), сумма считается равной нулю.
3. Результатом работы алгоритма становится модуль разности полученных двух сумм.
Пример. Дано число N = 2021. Алгоритм работает следующим образом:
1. Чётные цифры в записи: 2, 0, 2, их сумма равна 4.
2. Цифры на чётных местах: 0, 1, их сумма равна 1.
3. Модуль разности полученных сумм равен 3.
Результат работы алгоритма R = 3.
При каком наименьшем N в результате работы алгоритма получится R = 9?
