Преобразование логических выражений. Задание 15 ЕГЭ. Программный способ

Пример:

Для какого наименьшего целого неотрицательного числа А выражение

(y + 2x < A) ∨ (x > 30) ∨ (y > 20)

тождественно истинно, то есть принимает значение 1 при любых целых неотрицательных x и y?

Решение на языке Pascal:

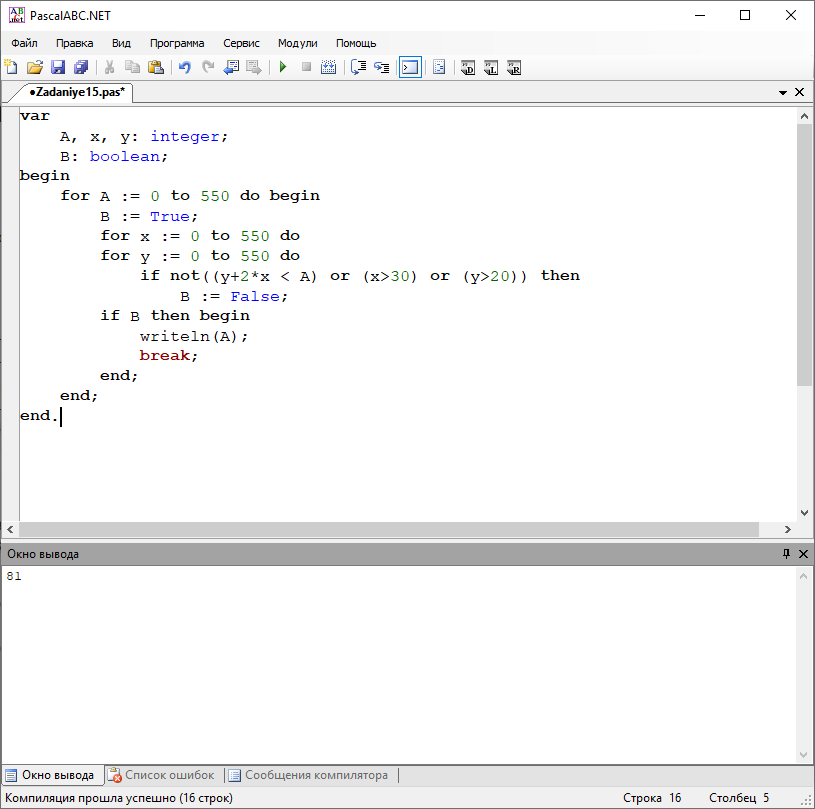
Особенности:

Количество переменных и циклов For в программе должно совпадать с количеством неизвестных в задании
Начальное и конечное значение цикла может меняться в зависимости от задачи (если после запуска, программа не выявила ошибок, но не вывела результат, попробуйте расширить диапазон значений цикла)
Если в программе сказано найти наибольшее значение, то замените цикл For ..to..do на For ..downto..do и, соответственно, поменяйте местами начальное и конечное значения.
В строке: if not((y+2*x < A) or (x>30) or (y>20)) then вводится выражение из задачи. Если исходное выражение содержит импликацию или эквивалентность, то его предварительно нужно преобразовать по формулам:

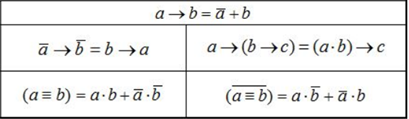
Напоминаю, что коньюнкция в Pascal обозначается and, а дизъюнкция or.

Пример 2:

Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Для какого наименьшего неотрицательного целого числа А формула

$((x\28 не равно 0) \vee (x\45 не равно 0)) arrow ((x\48=0) arrow (x\A не равно 0))$

тождественно истинна (то есть принимает значение 1 при любом неотрицательном целом значении переменной x)?

Решение:

Преобразуем формулу, заменив импликацию на дизъюнкцию:

((x and 28) = 0) and ((x and 45) = 0) or ((x and 48) = 0) or ((x and A)<>0)

Составим программу:

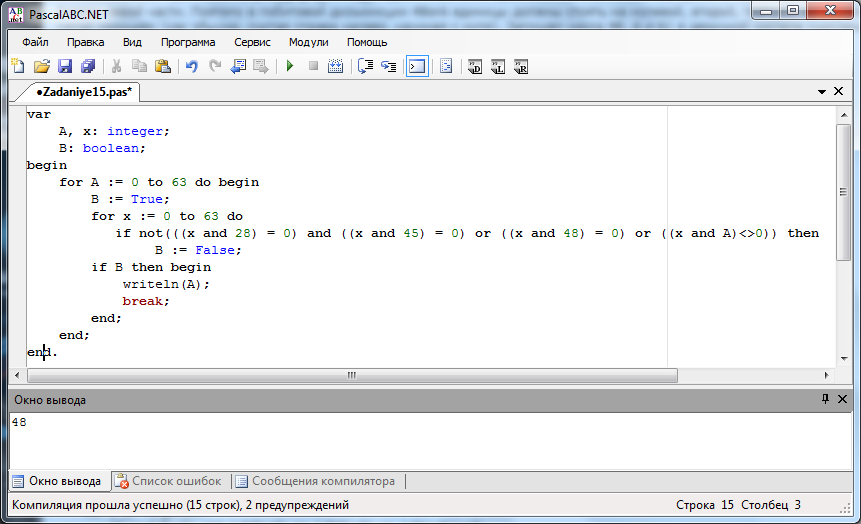
Внимание! Внимательно следите за скобками в выражении!

Задания для самостоятельного выполнения:

Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14&5 = 1110₂&0101₂ = 0100₂ = 4. Для какого наименьшего неотрицательного целого числа А формула x&51 = 0 \/ (x&11 = 0 → x&А ≠ 0) тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной х)?
Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14&5 = 1110₂&0101₂ = 0100₂ = 4. Для какого наибольшего неотрицательного целого числа А формула x&А ≠ 0 → ((x&17 = 0 /\ x&5 = 0)→ x&3 ≠ 0) тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной х)?
Для какого наименьшего целого неотрицательного числа А выражение (y + 2x < A) \/ (x> 30) \/ (y> 20) тождественно истинно, то есть принимает значение 1 при любых целых неотрицательных x и y?
Для какого наибольшего целого неотрицательного числа А выражение (2x + y ≠ 70) \/ (x < y) \/ (A < x) тождественно истинно, то есть принимает значение 1 при любых целых неотрицательных x и y?