Решение с использованием MS Excel.
Пример 1. Места в театре, на стадионе

Решение
1.Копируем данные с блокнота, вставляем в Excel, удаляем первую строку и разделяем данные по столбцам (данные-> текст по столбцам). Если данные корректно не разделяются, можно вначале выполнить разделение по столбцам, а после вставить скопированные значения. Или же в блокноте заменить все пробелы на «;» и далее также разделить текст по столбцам, но в качестве разделителя выбрать «;».
2.Выполняем сортировку. Так как по заданию нам необходимо найти минимальный ряд, то ряды мы сортируем по возрастанию. А место ищем максимальное, следовательно сортируем по убыванию (данные-> сортировка)
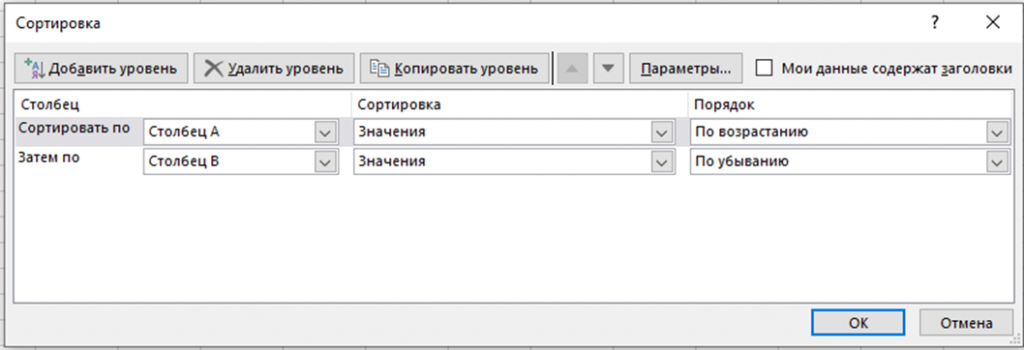
3. Чтобы у нас было два свободных места между занятыми, разница в соседних занятых местах должна быть равна 3. Таким образом, в столбце С вводим формулу:=ЕСЛИ(B1-B2=3;ИСТИНА;0). Ищем ближайшие места, удовлетворяющие условию:
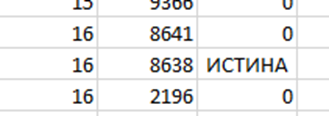
Ответ: 16 8640
Пример 2. Саженцы, деревья

Решение
1.Копируем, вставляем значения в Excel, сортируем по возрастанию.
2. Чтобы избавиться от повторяющихся ячеек: выделяем все значения-> Данные->удалить дубликаты.
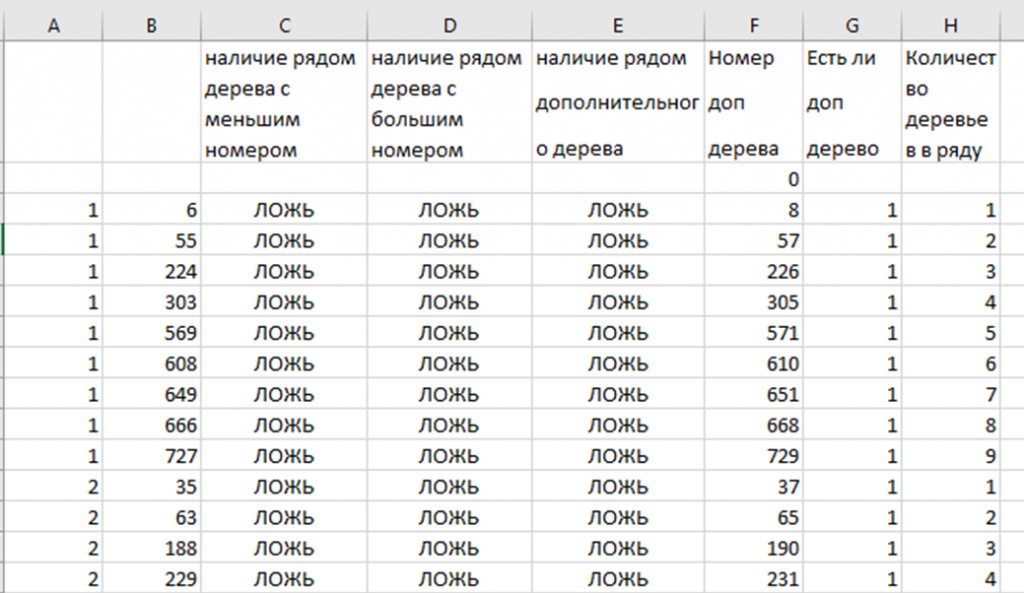
3.Далее заполняем формулами:
•С3=И(A2=A3;B3-B2<=2)
•D3 =И(A3=A4;B4-B3<=2)
•E3=И(A3=A2;B3-F2<=2
•F3=ЕСЛИ(ИЛИ(C3:E3);0;B3+2) – сумма-количество высаженных деревьев
•G3=ЕСЛИ(F3>0;1;0)
•H3=1
•H4= =ЕСЛИ(A3=A4;H3+G4;1) – ищем максимальное значение
4. Чтобы найти ряд, можно воспользоваться формулой:=ПОИСКПОЗ(19;H3:H9944;0)
Ответ: 9313 319
Пример 3. Подарочные коробки


Ответ: 174 10
Задачи для самостоятельного решения
Задача 1. Системный администратор раз в неделю создаёт архив пользовательских файлов. Однако объём диска, куда он помещает архив, может быть меньше, чем суммарный объём архивируемых файлов. Известно, какой объём занимает файл каждого пользователя. По заданной информации об объёме файлов пользователей и свободном объёме на архивном диске определите максимальное число пользователей, чьи файлы можно сохранить в архиве, а также максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Входные данные.
В первой строке входного файла находятся два числа: S – размер свободного места на диске (натуральное число, не превышающее 10 000) и N – количество пользователей (натуральное число, не превышающее 1000). В следующих N строках находятся значения объёмов файлов каждого пользователя (все числа натуральные, не превышающие 100), каждое в отдельной строке.
Запишите в ответе два числа: сначала наибольшее число пользователей, чьи файлы могут быть помещены в архив, затем максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Файлы к заданию: 26.txt
Задача 2. Для перевозки партии грузов различной массы выделен грузовик, но его грузоподъёмность ограничена, поэтому перевезти сразу все грузы не удастся. Грузы массой от 310 до 320 кг грузят в первую очередь. На оставшееся после этого место стараются взять как можно большее количество грузов. Если это можно сделать несколькими способами, выбирают тот способ, при котором самый большой из выбранных грузов имеет наибольшую массу. Если и при этом условии возможно несколько вариантов, выбирается тот, при котором наибольшую массу имеет второй по величине груз, и т.д. Известны количество грузов, масса каждого из них и грузоподъёмность грузовика. Необходимо определить количество и общую массу грузов, которые будут вывезены при погрузке по вышеописанным правилам.
Входные данные представлены в файле следующим образом. В первой строке входного файла записаны два целых числа: N – общее количество грузов и M – грузоподъёмность грузовика в кг. Каждая из следующих N строк содержит одно целое число – массу груза в кг. В ответе запишите два целых числа: сначала максимально возможное количество грузов, затем их общую массу.
Пример организации исходных данных во входном файле:
6 720
100
315
120
160
140
300
В данном случае сначала нужно взять груз массой 315 кг. Остается 405 кг. После этого можно вывезти ещё максимум 3 груза. Это можно сделать тремя способами: 100 + 120 + 140, 100 + 140 + 160, 100 + 120 + 160. Выбираем способ, при котором вывозится груз наибольшей возможной массы. Таких способов два: 100 + 120 + 160, 100 + 140 + 160. Из этих способов выбираем тот, при котором больше масса второго по величине груза, то есть 100 + 140 + 160. Всего получается 4 груза общей массой 715 кг. Ответ: 4 715.
Файлы к заданию: 26.txt
Задача 3. На вход программе поступает набор чисел в диапазоне [10; 10000]. Необходимо узнать сколько чисел в массиве находятся в диапазоне между средним значением и медианой, включая совпадающие с этими показателями значения.
Входные данные представлены в файле следующим образом. В первой строке записано нечетное число N – количество чисел, в каждой из последующих N строк число из обрабатываемой последовательности.
В качестве ответа дать одно число – количество найденных чисел.
Пример организации исходных данных во входном файле:
7
10
47
60
84
65
47
37
При таких исходных результатом является число 2. Среднее значение равно 50, медиана – 47
Медианой называется такое значение, что ровно половина из оставшихся элементов больше медианы и, соответственно, вторая половина меньше медианы.
Файлы к заданию: 26.txt
Задача 4. Каждый день Петр ест некоторое количество конфет. Так как Петр любит фантики от конфет, то он каждый такой фантик откладывает. Таким образом каждый день у него набирается некоторое количество фантиков.
Нашему герою интересно, какое максимальное количество фантиков он сможет собрать за K дней (необязательно идущих подряд) и минимальное количество фантиков, собранных за один из этих дней. Помогите нашему герою узнать эту информацию.
Входные и выходные данные.
В первой строке входного файла находятся два числа: N – Общее количество дней, на протяжении которых Петр собирал фантики (натуральное число, не превышающее 10 000) и K – количество дней, на протяжении которых Петр собрал максимально возможное количество фантиков (натуральное число, не превышающее 1000).
В следующих N строках находятся значения количества собранных фантиков (все числа натуральные, не превышающие 1000), каждое в отдельной строке.
Гарантируется, что N > K.
Запишите в ответе два числа: максимальное число фантиков, собранных Петей за K дней и минимальное количество собранных главным героем за один день
Пример входного файла:
5 3
60
30
50
40
10
При таких исходных данных Петр может собрать суммарно максимум 150 фантиков за 3 дня (40+50+60 = 150)
Наименьшие количество собранных главным героем фантиков за один день оказалось – 40
Файлы к заданию: 26.txt
Задача 5. В проекте «СкупойПлатитДважды» 1 января решено тратить на развитие 60% накоплений всех участников. При этом 20% самых богатых участников вносят 80% от своих накоплений, остальные участники вносят равный процент таким образом, чтобы общая сумма взносов всех участников составила 60%, обозначенные выше.
Запишите в ответе два целых числа: сумма взноса от всех «богатых» участников проекта и сумма взноса участника с самым небольшим размером накоплений.
Входные данные.
В первой строке входного файла находится число N – количество участников проекта (натуральное число, 20 ≤ N ≤ 1000). В следующих N строках находятся значения – размер накоплений всех пользователей (все числа натуральные, не превышающие 1000), каждое в отдельной строке.
Пример входного файла:
10
10
12
25
25
40
35
18
19
10
12
При таких исходных данных ответ должен содержать 2 числа – 60 и 4.
Примечание: в случае нецелого количества участников при нахождении 20% взять целую часть.
Файлы к заданию: 26.txt
Задача 6. В магазине Пятэльдодео на черную пятницу решено провести одну из двух акций.
Первая акция – 30% скидки на 70% самых дешевых товаров, 40% процентов скидки на оставшиеся товары.
Вторая акция – 40% скидки на 50% самых дешевых товаров, 35% процентов скидки на оставшиеся товары.
Определить, какая акция принесет больше выручки, если предположить, что все товары будут проданы.
В качестве ответа привести разницу в выручке двух акций и стоимость самого дорогого товара, реализованного при проведении самой выгодной. В форму записать целые части найденных чисел.
Входные данные.
В первой строке входного файла находится число N – количество товаров кратное 20 (натуральное число, 20 ≤ N ≤ 10000). В следующих N строках находятся значения – стоимость товаров (целое число не большее 1000).
Пример входного файла (все значения с новой строки):
20
4 13 4 23 22 20 8 6 5 12 48 22 50 12 63 23 4 8 9 11
При таких исходных данных ответ должен содержать 2 числа – 1 и 40.
Файлы к заданию: 26.txt
Задача 7. Организация купила для своих сотрудников все места в нескольких подряд идущих рядах на концертной площадке. Известно, какие места уже распределены между сотрудниками. Найдите ряд с наибольшим номером, в котором есть два соседних места, таких что слева и справа от них в том же ряду места уже распределены (заняты). Гарантируется, что есть хотя бы один ряд, удовлетворяющий условию.
Входные данные представлены в файле следующим образом. В первой строке входного файла находится одно число: N – количество занятых мест (натуральное число, не превышающее 10 000). В следующих N строках находятся пары чисел: ряд и место выкупленного билета, не превышающие 100000. В ответе запишите два целых числа: номер ряда и наименьший номер места из найденных в этом ряду подходящих пар.
Пример входного файла:
10
5 5
5 9
5 6
16 9
16 3
16 6
20 23
20 28
20 35
20 40
В данном примере есть следующие свободные места, удовлетворяющие условию: 7 и 8 в ряду 5, 4 и 5 в ряду 16, а также 7 и 8 в ряду 16. Выбираем наибольший номер ряда: 16 и наименьший номер места: 4. В ответе нужно указать: 16 4.
Файлы к заданию: 26.txt
Задача 8. Магазин предоставляет оптовому покупателю скидку по следующим правилам:
− на каждый второй товар ценой больше 200 рублей предоставляется скидка 30%;
− общая цена покупки со скидкой округляется вверх до целого числа рублей;
− порядок товаров в списке определяет магазин и делает это так, чтобы общая сумма скидки была наименьшей.
Вам необходимо определить общую цену закупки с учётом скидки и цену самого дорогого товара, на который будет предоставлена скидка.
Входные данные. Первая строка входного файла 26.txt содержит число N – общее количество купленных товаров. Каждая из следующих N строк содержит одно целое число – цену товара в рублях. В ответе запишите два целых числа: сначала общую цену покупки с учётом скидки, затем цену самого дорогого товара, на который предоставлена скидка.
Пример входного файла
7
225
160
380
95
192
310
60
В данном случае товары с ценой 60, 95, 160 и 192 не участвуют в определении скидки, остальные товары магазину выгодно расположить в таком порядке цен: 380, 225, 310. Скидка предоставляется на товар ценой 225. Его цена со скидкой составит 157,5 руб., после округления – 158 руб. Общая цена покупки составит: 60 + 95 + 160 + 192 + 158 + 380 + 310 = 1355 руб. Самый дорогой товар, на который будет получена скидка, стоит 225 руб. В ответе нужно записать числа 1355 и 225.
Файлы к заданию: 26.txt
Задача 9. Магазин предоставляет оптовому покупателю скидку по следующим правилам:
− на каждый второй товар ценой больше 200 рублей предоставляется скидка 30%;
− общая цена покупки со скидкой округляется вверх до целого числа рублей;
− порядок товаров в списке определяет магазин и делает это так, чтобы общая сумма скидки была наименьшей.
Вам необходимо определить общую цену закупки с учётом скидки и цену самого дорогого товара, на который будет предоставлена скидка.
Входные данные. Первая строка входного файла 26.txt содержит число N – общее количество купленных товаров. Каждая из следующих N строк содержит одно целое число – цену товара в рублях. В ответе запишите два целых числа: сначала общую цену покупки с учётом скидки, затем цену самого дорогого товара, на который предоставлена скидка.
Пример входного файла
7
225
160
380
95
192
310
60
В данном случае товары с ценой 60, 95, 160 и 192 не участвуют в определении скидки, остальные товары магазину выгодно расположить в таком порядке цен: 380, 225, 310. Скидка предоставляется на товар ценой 225. Его цена со скидкой составит 157,5 руб., после округления – 158 руб. Общая цена покупки составит: 60 + 95 + 160 + 192 + 158 + 380 + 310 = 1355 руб. Самый дорогой товар, на который будет получена скидка, стоит 225 руб. В ответе нужно записать числа 1355 и 225.
Файлы к заданию: 26.txt
10. Спутник «Фотон» проводит измерения солнечной активности, результат каждого измерения представляет собой натуральное число. Перед обработкой серии измерений из неё исключают K наибольших и K наименьших значений (как недостоверные). По заданной информации о значении каждого из измерений, а также количестве исключаемых значений, определите наибольшее достоверное измерение, а также целую часть среднего значения всех достоверных измерений.
Входные и выходные данные.
В первой строке входного файла находятся два числа, записанные через пробел: N – общее количество измерений (натуральное число, не превышающее 10 000) и K – количество исключаемых минимальных и максимальных значений. В следующих N строках находятся значения каждого из измерений (все числа натуральные, не превышающие 1000), каждое в отдельной строке.
Запишите в ответе два числа: сначала наибольшее достоверное измерение, а затем целую часть среднего значения всех достоверных измерений.
Пример входного файла:
10 2
34
50
43
44
23
9
39
5
38
36
При таких исходных данных ответ должен содержать 2 числа – 43 и 35. Пояснение: будут отброшены значения 5, 9, 44, 50. Тогда наибольшее оставшееся значение равно 43, а среднее значение из оставшихся равно (23+34+36+38+39+43):6 = 35,5.
Файлы к заданию: 26.txt
11.

12. В лесополосе осуществляется посадка деревьев. Причем деревья высаживают рядами на одинаковом расстоянии. Между соседними деревьями в одном ряду расстояние метров.
Через какое-то время осуществляется аэросъемка, в результате которой определяется, какие деревья прижились. Для успешного перекрестного опыления необходимо, чтобы дерево было на расстоянии не более метров от прижившегося дерева, иначе оно не будет плодоносить. При аэросъемке была совершена ошибка — одно и то же дерево могло быть снято дважды. Определите, какое минимальное количество деревьев нужно посадить, чтобы все деревья могли плодоносить, и номер ряда, в котором необходимо посадить максимальное количество деревьев. Если таких рядов несколько, нужно найти номер первого из них.
Входные данные:
В первой строке входного файла находится число — количество занятых мест. Каждая из следующих
строк содержит два натуральных числа, не превышающих
: номер ряда и номер занятого места.
Выходные данные:
Два целых неотрицательных числа: минимальное количество деревьев которое нужно посадить, чтобы все деревья могли плодоносить, и минимальный номер ряда, в котором необходимо посадить максимальное количество деревьев.
Пример входного файла:
7
4 2
7 5
4 5
5 1
7 1
5 5
7 10
В этом случае достаточно посадить дерева в позициях
,
,
и
. Наибольшее количество деревьев нужно посадить в 7-м ряду. Ответ:
.
13. В магазине для упаковки подарков есть N кубических коробок. Самой интересной считается упаковка подарка по принципу матрёшки — подарок упаковывается в одну из коробок, та в свою очередь в другую коробку и т. д. Одну коробку можно поместить в другую, если длина её стороны хотя бы на 3 единицы меньше длины стороны другой коробки.
Определите наибольшее количество коробок, которое можно использовать для упаковки одного подарка, и максимально возможную длину стороны самой маленькой коробки, где будет находиться подарок. Размер подарка позволяет поместить его в самую маленькую коробку.
В первой строке входного файла находится число N — количество коробок в магазине (натуральное число, не превышающее 10 000). В следующих N строках находятся значения длин сторон коробок (все числа натуральные, не превышающие 10 000), каждое — в отдельной строке.
Запишите в ответе два целых числа: сначала наибольшее количество коробок, которое можно использовать для упаковки одного подарка, затем максимально возможную длину стороны самой маленькой коробки в таком наборе.
Пример входного файла:
5
43
40
32
40
30
Пример входного файла приведён для пяти коробок и случая, когда минимальная допустимая разница между длинами сторон коробок, подходящих для упаковки «матрёшкой», составляет 3 единицы.
При таких исходных данных условию задачи удовлетворяют наборы коробок с длинами сторон 30, 40 и 43 или 32, 40 и 43 соответственно, т. е. количество коробок равно 3, а длина стороны самой маленькой коробки равна 32.
