ФИПИ Задание 1.5.1 базовый уровень. Рекомендуемое время для выполнения — 3 мин
Теоретические сведения
Логические операции

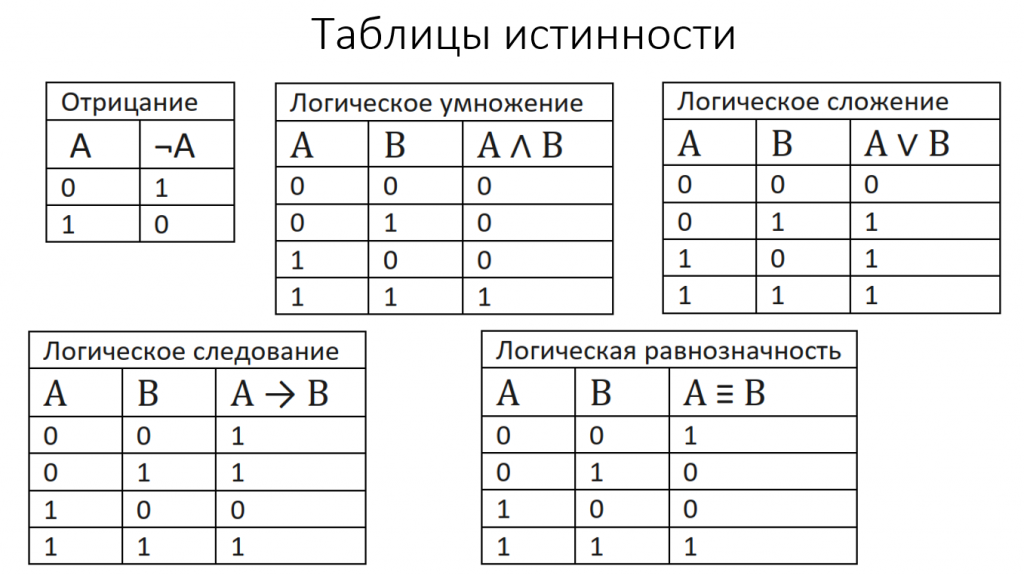
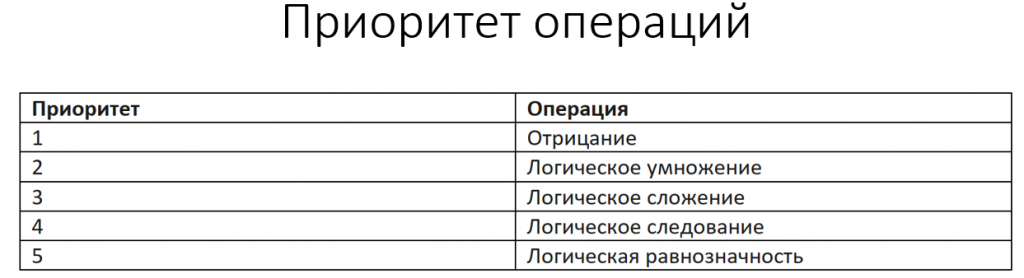

Тип 1. Монотонные функции
Логическая функция F задаётся выражением:
(¬x ∧ y ∧ z) ∨ (¬x ∧ ¬y ∧ z) ∨ (¬x ∧ ¬y ∧ ¬z).
На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна. Определите, какому столбцу таблицы истинности функции F соответствует каждая
| Перем. 1 | Перем. 2 | Перем. 3 | Функция |
| ??? | ??? | ??? | F |
| 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу, затем – буква, соответствующая второму столбцу, и т. д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение. Рассмотрим нашу функцию. Она состоит из трех выражений в скобках, соединенных между собой дизъюнкцией. Если мы посмотрим на значение F в таблице, то заметим, что оно всегда равно 1. Дизъюнкция дает 1, если хотя бы одно из выражений равно 1.
Рассмотрим первое выражение в скобках(¬x ∧ y ∧ z): оно будет истинно только в случае: х=0, у=1, z=1
Рассмотрим второе выражение в скобках(¬x ∧ ¬y ∧ z): оно будет истинно только в случае: х=0, у=0, z=1
Рассмотрим первое выражение в скобках(¬x ∧ ¬y ∧ ¬z): оно будет истинно только в случае: х=0, у=0, z=0
Сопоставим полученные значения с таблицей. Перем.1 будет соответствовать z (так как только z в одном случае равна 0, а в двух других 1), Перем.2 будет соответствовать х (так как х во всех трех случаях равна 0), Перем.3 будет соответствовать у.
Ответ: zxy
Тип 2. Немонотонные функции
Логическая функция F задаётся выражением (¬z)∧x ∨ x∧y. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| Перем. 1 | Перем. 2 | Перем. 3 | Функция |
| ??? | ??? | ??? | F |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая 1-му столбцу; затем – буква, соответствующая 2-му столбцу; затем – буква, соответствующая 3-му столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение. Составим свою таблицу истинности для заданного выражения и сравним с исходной:
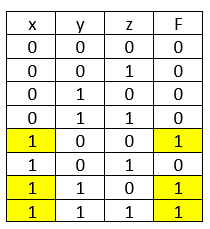
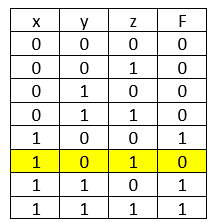
Ответ: zyx
Тип 3. Строки с пропущенными значениями
Логическая функция F задаётся выражением (x ∨ y) → (z ≡ x).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z.
| Переменная 1 | Переменная 2 | Переменная 3 | Функция |
| ??? | ??? | ??? | F |
| 0 | 0 | 0 | |
| 0 | 0 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Задание решается аналогичным построением таблицы истинности и сравнением ее с исходной.
Программный способ решения
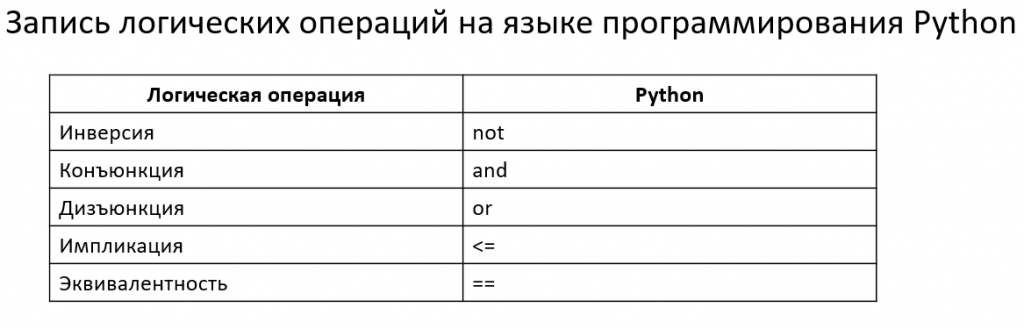
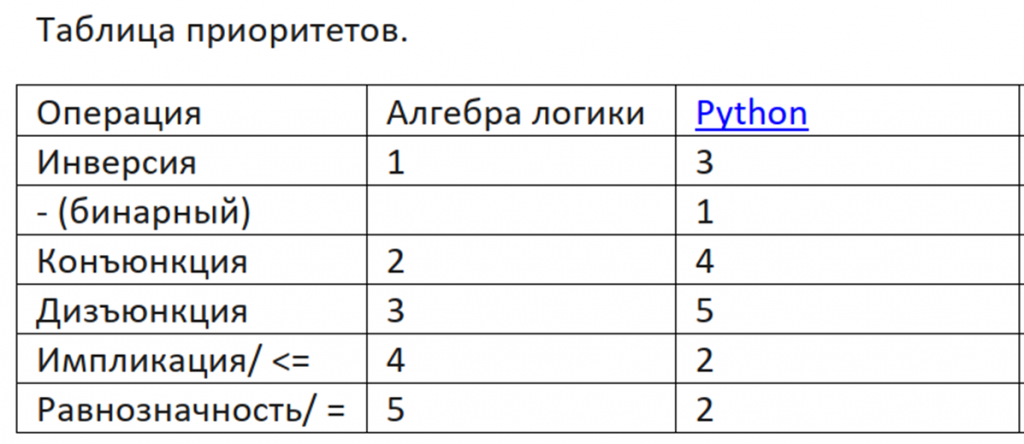
1 способ
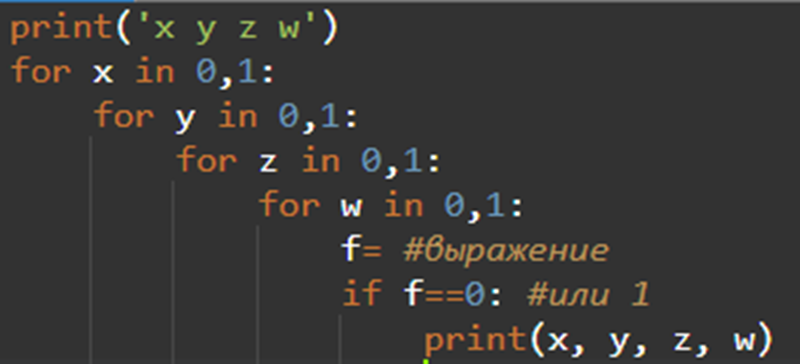
Данный способ выводит не готовый ответ, а таблицу истинности для заданных условий. Чтобы получить ответ, необходимо сравнить таблицу с исходной и правильно сопоставить переменные.
2 способ

Данный способ решения выводит готовый результат
