Задача.
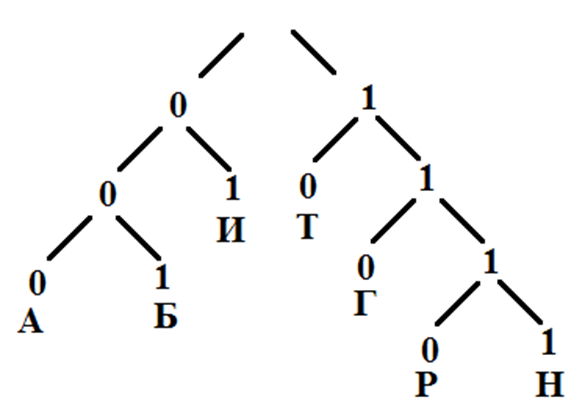
По каналу связи передаются сообщения, содержащие только семь букв: А, Б, Г, И, Н, Р, Т. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: Г — 110, И — 01, Т — 10. Какое наименьшее количество двоичных знаков потребуется для кодирования слова БАРАБАН?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Для решения задач будем строить дерево Фано
Дерево Фано для двоичного кодирования начинается с двух направлений, которые означают 0(ноль) и 1(единицу) (цифры двоичного кодирования).
От каждого направления можно также рисовать только два направления: 0(ноль) и 1(единицу) и т.д. Для удобства будем рисовать 1(единицу) только вправо, а 0(ноль) только влево.
В конце каждой ветки можно располагать букву, которую мы хотим закодировать, но если мы расположили букву, от этой ветки больше нельзя делать новых ответвлений.
Вначале расположим буквы, которые уже имеют код (Г, И, Т), на Дереве Фано.
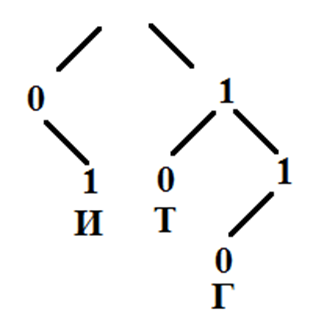
Продолжим дерево до тех пор, пока не будет возможности закодировать остальные буквы (А, Б, Р, Н). Так как буквы Б и А встречаются в слове БАРАБАН несколько раз, то для их кодирования выберем наименьший код, чтобы конечная сумма кода была тоже наименьшей. Таким образом, А – 000(3 знака), Б – 001(3 знака), Р – 1110(4 знака), Н – 1111(4 знака). Количество двоичных знаков: 3+3+4+3+3+3+4 = 23.