Тип 1. Исполнители на плоскости
Вариант 1.Исполнитель Чертежник имеет перо, которое можно поднимать, опускать и перемещать. При перемещении опущенного пера за ним остается след в виде прямой линии. У исполнителя существуют следующие команды:
Сместиться на вектор (а, b) – исполнитель перемещается в точку, в которую можно попасть из данной, пройдя а единиц по горизонтали и b – по вертикали.
Запись: Повторить 5[Команда 1 Команда 2] означает, что последовательность команд в квадратных скобках повторяется 5 раз.
Чертежник находится в начале координат. Чертежнику дан для исполнения следующий алгоритм:
Сместиться на вектор (5,2)
Сместиться на вектор (-3, 3)
Повторить 3[Сместиться на вектор (1,0)]
Сместиться на вектор (3, 1)
На каком расстоянии от начала координат будет находиться исполнитель Чертежник в результате выполнения данного алгоритма?
Решение. Конечная точка будет обладать координатами по оси x и y. Эти координаты можно складывать независимо друг от друга.
Найдём значение x: 5 – 3 + 1 + 1 + 1 + 3 = 8. Найдём значение y: 2 + 3 + 1 = 6.

Вариант 2.
Исполнитель Робот действует на клетчатой доске, между соседними клетками которой могут стоять стены. Робот передвигается по клеткам доски и может выполнять команды 1 (вверх), 2 (вниз), 3 (вправо) и 4 (влево), переходя на соседнюю клетку в направлении, указанном в скобках. Если в этом направлении между клетками стоит стена, то Робот разрушается. Робот успешно выполнил программу
1132432
Какую последовательность из трех команд должен выполнить Робот, чтобы вернуться в ту клетку, где он был перед началом выполнения программы, и не разрушиться вне зависимости от того, какие стены стоят на поле?
Решение. Если робот пойдёт назад тем же путём, каким пришёл в конечную клетку, то он точно не разрушится. Группа команд 1324 круговая, поэтому её можно откинуть. До конечной клетки робот прошёл путём 132. Значит, чтобы попасть обратно, ему нужно заменить команды на противоположные (241) и записать их справа налево: 142.
Ответ: 142.
Вариант 3.
Исполнитель Робот ходит по клеткам бесконечной вертикальной клетчатой доски, переходя по одной из команд вверх, вниз, вправо, влево в соседнюю клетку в указанном направлении. Робот выполнил следующую программу:
вправо
вниз
вправо
вверх
влево
вверх
вверх
влево
Укажите наименьшее возможное число команд, которое необходимо для того, чтобы Робот вернулся в ту же клетку, из которой начал движение.
Решение. Заметим, что пары команд «вверх-вниз» и «влево-вправо» дают нулевой эффект, то есть, не перемещают Робота, поэтому все такие пары можно выкинуть из программы, вдобавок, поскольку стенок нет, все равно где стоят парные команды в программе. Вычеркнув все пары, видим, что остались только команды вверх, вверх. Их две.
Ответ: 2.
Вариант 4. Исполнитель КУЗНЕЧИК живёт на числовой оси. Начальное положение КУЗНЕЧИКА – точка 10. Система команд Кузнечика:
Вперед 7 – Кузнечик прыгает вперёд на 7 единиц,
Назад 4 – Кузнечик прыгает назад на 4 единицы.
Какое наименьшее количество раз должна встретиться в программе команда «Назад 4», чтобы Кузнечик оказался в точке 43?
Решение.
Обозначим через х количество команд «Вперед 7» в программе, а через у – количество команд «Назад 4», причём х и y могут быть только неотрицательными целыми числами.
Для того, чтобы КУЗНЕЧИК попал в точку 43 из точки 10, должно выполняться условие: 7х – 4у = 43 – 10. Упростим: 7х – 33 = 4у. Подбираем наименьшее возможное у – при х = 7, у = 4.
Ответ: 4
Тип 2. Посимвольное двоичное преобразование (ФИПИ 1.6.1 базовый уровень)
Вариант 1. На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописываются справа ещё два разряда по следующему правилу:
а) складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;
б) над этой записью производятся те же действия — справа дописывается остаток от деления суммы цифр на 2.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.
Укажите минимальное число R, которое превышает 43 и может являться результатом работы алгоритма. В ответе это число запишите в десятичной системе.
Решение. Если в числе было нечётное количество единиц, то в конец допишется 10. Если количество единиц чётное, то допишется 00. Рассмотрим числа, большие 43. 4410 = 1011002 — не может являться результатом работы алгоритма,
4510 = 1011012 — не может являться результатом работы алгоритма,
4610 = 1011102 — может являться результатом работы алгоритма, количество единиц (кроме последних двух разрядов) нечетное, и в последних двух разрядах 10.
Ответ: 46.
Вариант 2. Автомат обрабатывает натуральное число N (128 ≤ N ≤ 255) по следующему алгоритму:
1. Строится восьмибитная двоичная запись числа N.
2. Все цифры двоичной записи заменяются на противоположные (0 на 1, 1 на 0).
3. Полученное число переводится в десятичную запись.
4. Из исходного числа вычитается полученное, разность выводится на экран.
Пример. Дано число N = 131. Алгоритм работает следующим образом:
1. Восьмибитная двоичная запись числа N: 10000011.
2. Все цифры заменяются на противоположные, новая запись: 01111100.
3. Десятичное значение полученного числа: 124.
4. На экран выводится число: 131 – 124 = 7.
Какое число нужно ввести в автомат, чтобы в результате получилось 185?
Решение. Заметим, что инверсия двоичной восьмибитной записи числа в сумме с исходным числом дает 11111111, то есть 255. (В исходном примере: 10000011 + 01111100 = 11111111.) Следовательно, если исходное число равно N, то инвертированное число равно 255 − N. Затем автомат осуществляет вычитание, вычисляя 2N − 255.
Поэтому, чтобы найти число, которое нужно ввести в автомат для получения 185, нужно решить уравнение 2N − 255 = 185. Тем самым, искомое число равно 220.
Ответ: 220.
Вариант 3. Автомат обрабатывает натуральное число N по следующему алгоритму:
1. Строится двоичная запись числа N.
2. Удаляется первая слева единица и все следующие непосредственно за ней нули. Если после этого в числе не остаётся цифр, результат этого действия считается равным нулю.
3. Полученное число переводится в десятичную запись.
4. Новое число вычитается из исходного, полученная разность выводится на экран.
Пример. Дано число N = 11. Алгоритм работает следующим образом.
1. Двоичная запись числа N: 1011.
2. Удаляется первая единица и следующий за ней ноль: 11.
3. Десятичное значение полученного числа 3.
4. На экран выводится число 11 – 3 = 8.
Сколько разных значений будет показано на экране автомата при последовательном вводе всех натуральных чисел от 10 до 1000?
Решение. Заметим, что при удалении первой единицы и всех стоящих сразу за ней нулей из числа вычитается 2 в степени, равной номеру старшего разряда в двоичной записи числа. Значит, нужно найти количество степеней двойки, которые находятся между 10 и 1000. Также необходимо учесть, что числа от 10 до 15 будут соответствовать предыдущей степени двойки. Значит, к количеству степеней двойки, входящих в диапазон чисел от 10 до 1000, необходимо добавить единицу. Всего в диапазоне от 10 до 1000 шесть степеней двойки. Следовательно, будет показано 6 + 1 = 7 различных чисел.
Ответ: 7.
Тип 3. Исполнитель вычислитель. Арифмометры (ФИПИ 1.6.1, 1.6.3 базовый уровень)
Вариант 1. Исполнитель КВАДРАТОР имеет только две команды, которым присвоены номера:
1. возведи в квадрат
2. прибавь 1
Выполняя команду номер 1, КВАДРАТОР возводит число на экране в квадрат, а выполняя команду номер 2, прибавляет к этому числу 1. Напишите программу, содержащую не более 4 команд, которая из числа 1 получает число 17. Укажите лишь номера команд.
(Например, программа 12122 — это программа: возведи в квадрат
прибавь 1
возведи в квадрат
прибавь 1
прибавь 1 ,которая преобразует число 1 в число 6).
Решение. Не любое число является квадратом целого числа, поэтому, если мы пойдём от числа 17 к числу 1, тогда однозначно восстановим программу. Полученные команды будут записываться справа налево.
1) Число 17 не является квадратом, значит, оно получено добавлением единицы к числу 16: 17 = 16 + 1 (команда 2).
2) Т. к. мы хотим получить не более 4 команд, то для получения числа 16 возведём в квадрат 4: 16 = 42 (команда 1).
Повторим рассуждение 2) для числа 4: 4 = 22 (команда 1), а для числа 2 применим рассуждение 1): 2 = 1 + 1 (команда 2). Тогда окончательно получаем ответ: 2112.
Посимвольное десятичное преобразование (ФИПИ 1.6.1 базовый уровень)
Вариант 1. Автомат получает на вход трёхзначное число. По этому числу строится новое число по следующим правилам.
1. Складываются первая и вторая, а также вторая и третья цифры исходного числа.
2. Полученные два числа записываются друг за другом в порядке убывания (без разделителей).
Пример. Исходное число: 348. Суммы: 3 + 4 = 7; 4 + 8 = 12. Результат: 127. Укажите наименьшее число, в результате обработки которого автомат выдаст число 1412.
Решение. Пусть 12 = 3 + 9, тогда 14 выгодно разбить на сумму чисел 9 и 5. Наименьшее исходное число, удовлетворяющее условиям задачи: 395.
Ответ: 395.
Вариант 2. Автомат получает на вход нечётное число X. По этому числу строится трёхзначное число Y по следующим правилам.
1. Первая цифра числа Y (разряд сотен) — остаток от деления X на 4.
2. Вторая цифра числа Y (разряд десятков) — остаток от деления X на 3.
3. Третья цифра числа Y (разряд единиц) — остаток от деления X на 2.
Пример.
Исходное число: 63179. Остаток от деления на 4 равен 3; остаток от деления на 3 равен 2; остаток от деления на 2 равен 1. Результат работы автомата: 321.
Укажите наименьшее двузначное число, при обработке которого автомат выдаёт результат 301.
Решение. Можно заметить, что подходит число 15, а все остальные двузначные числа меньшие 15 либо делятся на 2, либо не делятся на 3.
Ответ: 15.
Разные задачи (ФИПИ 1.6.1 базовый уровень)
Вариант 1. На экране есть два окна, в каждом из которых записано по числу. Исполнитель СУММАТОР имеет только две команды, которым присвоены номера:
1. Запиши сумму чисел в первое окно
2. Запиши сумму чисел во второе окно
Выполняя команду номер 1, СУММАТОР складывает числа в двух окнах и заменяет этой суммой число в первом окне, а выполняя команду номер 2, заменяет этой суммой число во втором окне. Напишите программу, содержащую не более 5 команд, которая из пары чисел 1 и 2 получает пару чисел 13 и 4. Укажите лишь номера команд.
Например, программа 21211 – это программа:
Запиши сумму чисел во второе окно
Запиши сумму чисел в первое окно
Запиши сумму чисел во второе окно
Запиши сумму чисел в первое окно
Запиши сумму чисел в первое окно
которая преобразует пару чисел 1 и 0 в пару чисел 8 и 3.
Решение. Удобней будет идти от конца к началу. Обе команды сохраняют одно число неизменным, значит, в паре 13 и 4 тоже есть число из предыдущей пары. Т. к. 13 > 4, то 4 не изменилось, а значит, 13 = 9 + 4. Эта пара получена командой 1 из пары 9 и 4. Аналогично для 9: 9 = 5 + 4, команда 1 из пары 5 и 4. Аналогично для 5: 5 = 1 + 4, команда 1 из пары 1 и 4. Поскольку 1 < 4, то число 4 получено как 4 = 1 + 3, т. е. командой 2 из пары 1 и 3. Аналогично рассуждаем для 3: 3 = 1 + 2, командой 2 из пары 1 и 2. Окончательно, последовательность команд: 22111.
Вариант 2. Алгоритм получает на вход натуральное число N > 1 и строит по нему новое число R следующим образом:
1. Если исходное число кратно 2, оно делится на 2, в противном случае из него вычитается 1.
2. Если полученное на предыдущем шаге число кратно 3, оно делится на 3, в противном случае из него вычитается 1.
3. Если полученное на предыдущем шаге число кратно 5, оно делится на 5, в противном случае из него вычитается 1.
4. Число, полученное на шаге 3, считается результатом работы алгоритма.
Пример. Дано число N = 22. Алгоритм работает следующим образом:
1. Число 22 кратно 2, оно делится на 2, получается 11.
2. Число 11 не кратно 3, из него вычитается 1, получается 10.
3. Число 10 кратно 5, оно делится на 5, получается 2.
4. Результат работы алгоритма R = 2.
Сколько существует различных натуральных чисел N, при обработке которых получится R = 1?
Решение. Рассмотрим работу алгоритма в обратном порядке:
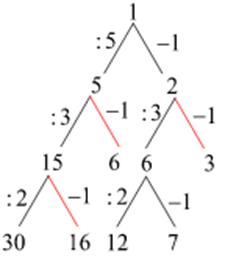
Таким образом, подходят три числа: 7, 12 и 30.
Ответ: 3.
Вариант 3. Автомат получает на вход два двузначных шестнадцатеричных числа. В этих числах все цифры не превосходят цифру 6 (если в числе есть цифра больше 6, автомат отказывается работать). По этим числам строится новое шестнадцатеричное число по следующим правилам.
1. Вычисляются два шестнадцатеричных числа – сумма старших разрядов полученных чисел и сумма младших разрядов этих чисел.
2. Полученные два шестнадцатеричных числа записываются друг за другом в порядке возрастания (без разделителей).
Пример. Исходные числа: 66, 43. Поразрядные суммы: A, 9. Результат: 9A.
Определите, какое из предложенных чисел может быть результатом работы автомата.
Ответ:
7B
8D
412
95
Решение. Если каждая цифра не превосходит 6, то максимально возможное число при сложении будет = 12, что в шестнадцатеричной системе соответствует С. Соответственно вариант 8D не подходит, так как D>C. Вариант 412 не может быть, так как в шестнадцатеричной системе 12 записывается как C. В числе 95 – цифры не расположены по возрастанию. Следовательно, правильный ответ 7В
