Пример 1:

Решение:
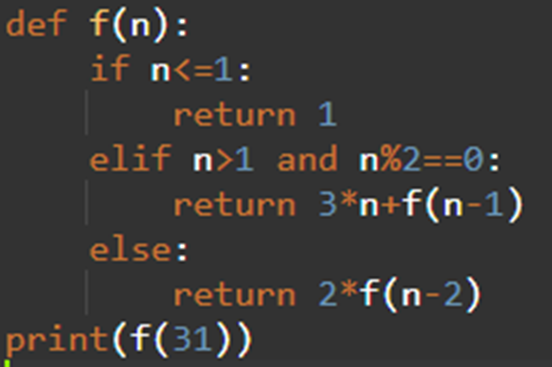
Ответ: 32768
Встроенная мемоизация (lru_cache)
В ряде задач из-за большого количества вызовов рекурсии, если запустить решение без оптимизаций, ждать результат придется очень долго. Эту проблему можно решить путем мемоизации (это техника оптимизации, которая позволяет сохранять результаты функций с целью избежать повторных вычислений).
Пример 2:

Решение:
from functools import lru_cache
@lru_cache(None)
def F(n):
if n < 3:
return 2
if n % 2 == 0:
return F(n-2) – F(n-1) + 2
else:
return F(n-1) – F(n-2) – 2
print(F(200) – F(193) + F(195))
Применение декоратора lru_cache значительно упрощает мемоизацию. Однако, надо понимать, что теперь при вызове функции F сначала вызывается функция lru_cache, то есть стек заполняется в два раза быстрее – на каждый вызов F для новых параметров в стек сначала добавляется состояние функции lru_cache и потом состояние функции F.
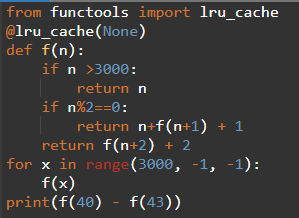
Пример 3.
В задачах, где расхождение параметра вычисляемой функции и параметра заданного в описании функции (в данном примере 40 и 3000) слишком большое, применение только декоратора lru_cache не позволит решить задачу. Программа все равно выдаст ошибку о том что превышен предел рекурсии. В этом случае, перед выводом результата, можно воспользоваться последовательным сохранением всех значений функции в обратном порядке