Пример:
Квадрат разлинован на N× Nклеток (1 < N< 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз– в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота.
В «угловых» клетках поля – тех, которые справа и снизу ограничены стенами, Робот не может продолжать движение, поэтому накопленная сумма считается итоговой. Таких конечных клеток на поле может быть несколько, включая правую нижнюю клетку поля. При разных запусках итоговые накопленные суммы могут различаться.
Определите максимальную и минимальную денежные суммы, среди всех возможных итоговых сумм, которые может собрать Робот, пройдя из левой верхней клетки в конечную клетку маршрута.
В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N× N, каждая ячейка которой соответствует клетке квадрата. Внутренние и внешние стены обозначены утолщёнными линиями.
Решение
1). Выделяем всю таблицу -> копируем-> вставляем ниже только форматирование
2). Определяем «мертвые» клетки – это клетки из которых робот не может никаким образом добраться до конечной клетки. В этих клетках считать результат не имеет смысла, поэтому их можно выделить контрастным цветом и не заполнять. В данном задании таких нет.
3). Определяем стартовые клетки (их может быть несколько!!!) и в каком направлении может двигаться робот. В данном случае он движется с левой верхней клетки вправо и вниз. Следовательно, левую верхнюю клетку просто копируем с таблицы выше (если стартовых клеток несколько, в них также просто копируем значение из таблицы). В ячейки вдоль левой границы Робот сможет попасть только сверху, поэтому в них формула будет следующая:

Растягиваем формулу в последующие ячейки и копируем во все ячейки вдоль левой стены. Для удобства выделяем заполненные ячейки заливкой. Аналогично поступаем с ячейками вдоль верхней границы:
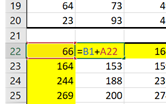
4). Находим максимум для остальных клеток. Так как в остальные ячейки таблицы мы уже можем попасть двумя способами – из верхней ячейки либо из левой, воспользуемся функцией МАКС.

5). Для нахождения ответа, необходимо внимательно перечитать задание и определить конечную клетку маршрута (их тоже может быть несколько!). В ответ записываем значение из конечной клетки маршрута (или максимум из всех конечных клеток маршрута).
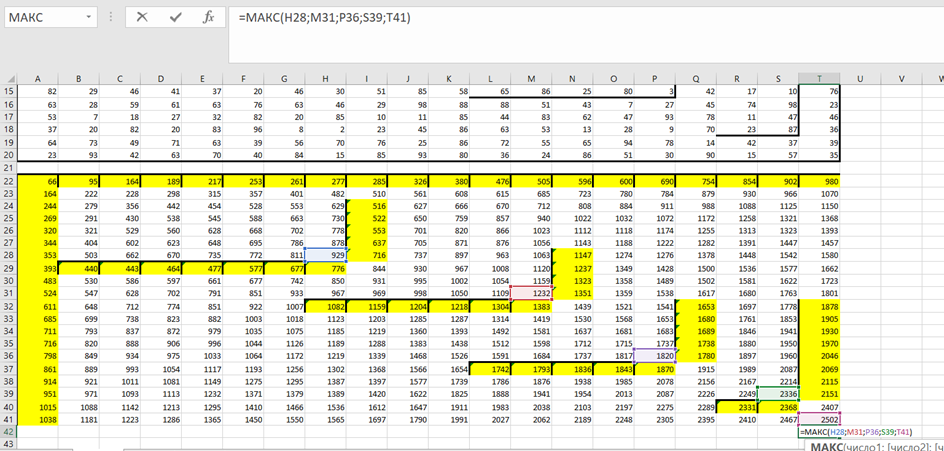
6). Для нахождения минимального значения, достаточно воспользоваться функцией замены (CTRL+F) и заменить МАКС на МИН.
Задания для самостоятельного решения
