Одна сотая часть числа называется процентом. Например, 1% от 4 это 0,04.
– Основные задачи на проценты – это:
– 1. Нахождение процентов данного числа.
Чтобы найти р % от а, надо а*0,01р
– 2. Нахождение числа по его процентам.
Если известно, что р% числа равно b, то а = b: 0,01р
– 3. Нахождение процентного отношения чисел.
Чтобы найти процентное отношение чисел, надо отношение этих чисел умножить на 100%: а/b *100
Примеры решения задач
Задача 1
При оплате услуг через платежный терминал взымается комиссия 5%. Терминал принимает суммы кратные 10 рублям. Аня хочет положить на счет своего мобильного телефона не меньше 300 рублей. Какую минимальную сумму она должна положить в приемное устройство данного терминала?
Решение:
300 * 0,05= 15 р – комиссия
300 + 15 = 315 сумма вместе с комиссией;
320 р – надо положить на счет.
Задача 2 (из задач учеников)
На покупку планшета взяли кредит 20000 р на 1 год под 16 % годовых. Вычислите, сколько денег необходимо вернуть банку, какова ежемесячная сумма выплат?
Решение:
20000*0,16 = 3200 – один год
20000 + 3200 = 23200 р
23200:12= 1933 р
Задача 3 ( ЕГЭ )
Мобильный телефон стоил 5000 рублей. Через некоторое время цену на эту модель снизили до 3000 рублей. На сколько процентов была снижена цена?
Решение:
5000 – 3000 = 2000 – на столько снижена цена на телефон
2000: 5000 *100 = 2:5 *100 = 0,4 *100 = 40 %
Ответ: на 40 %.
Решение задач на проценты с помощью пропорций
Задачи на проценты модно решать с помощью пропорций. Если A — это целое, которое принимаем за 100%, p% от него равны N, то можно составить пропорцию
Если есть одно неизвестное N, p% или A, то его можно найти из этой пропорции через две другие величины.
Из пропорции получаем формулы для нахождения каждого её члена через остальные:
Примеры
Задача 1: В школьной библиотеке 8400 книг, из них 5460 учебников. Какой прцент учебников в школьной библиотеке?
Решение: Общее количество книг в библиотеке 8400 — это число принято за 100%. Количество учебников 5460 составляет p% от общего числа книг. Составим пропорцию:
Найдем из этой пропорции p:
p%=(5460⋅100%)/8400=65%
Значит, в библиотеке 65% учебников.
Ответ: 65%
Задача 3: Вода составляет 76% картофеля. Сколько килограммов воды в 35 кг картофеля?
Решение: Вся масса картофеля принимается за 100% и равна 35 кг. Воды в ней 76% и массу воды надо найти. Обозначим её за N и составим пропорцию:
Найдем из этой пропорции N:
N=(76⋅35)/100=26,6
Ответ: 26,6
Задачи на смеси и сплавы
На выпускных экзаменах встречается много задач на смеси и сплавы. При решении таких задач мы используем таблицу.
Таблица для решения задач имеет вид (на доске)
Наименование веществ, растворов, смесей, сплавов |
% содержание вещества(доля содержания вещества) |
Масса раствора(смеси, сплава) |
Масса вещества |
Задача 4
Смешали 8 литров 15-процентного водного раствора некоторого вещества с 12 литрами 25-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение:
% содержания вещества |
Масса раствора |
Масса вещества |
|
1 раствор |
15% = 0,15 |
8 л |
8 *0,15 |
2 раствор |
25% = 0,25 |
12 л |
12 * 0,25 |
смесь |
X |
8 + 12 = 20 л |
20 x |
Сумма масс некоторого вещества в двух первых растворах (то есть в первых двух строчках) равна массе этого вещества в полученном растворе (третья строка таблицы):
20 x = 8*0,15 + 12 * 0,25
20 x = 1,2 + 3 = 4, 2
x = 4,2 : 20 = 0,21 = 21 %
Ответ: 21 %.
Старинный способ решения задач на смеси, сплавы и растворы (правило креста).
Впервые о нем было упомянуто в первом печатном учебнике математики Леонтия Магницкого.
Данный способ применялся купцами и ремесленниками при решении различных практических задач. Но в задачниках и различных руководствах для мастеров и торговцев никаких обоснований и разъяснений не приводилось. Просто давался рецепт решения: либо рисовалась схема, либо словесно описывалась последовательность действий — поступай так и получишь ответ.
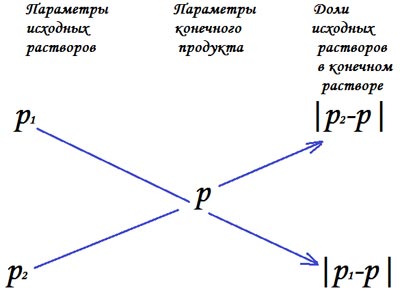
Задача 5.
Один раствор содержит 20 % соли, а второй – 70 %. Сколько граммов первого и второго раствора нужно взять, чтобы получить 100 г 50% раствора.
Решение:
Применим правило “креста”.
Составим схему:
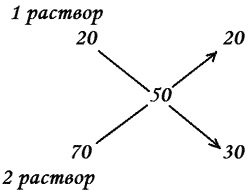
Значит, 100 г смеси составляют 20 + 30 = 50 частей.
100 : ( 20 + 30 ) = 2 г – на 1 часть.
2 * 20 = 40 г – 20% раствора
2 * 30 = 60 г – 70 % раствора
Ответ: 40 г- 20 % раствора; 60 г- 70 % раствора.
Задача 6.
Первый сплав содержит 10 % меди, второй – 25 % меди. Из этих двух сплавов получили третий сплав массой 30 кг, содержащий 20 % меди. Какое количество каждого сплава было использовано?
Решить задачу разными способами: системой уравнений, линейным уравнением, “крестом”.
(по рядам.)
1 способ: (система уравнений)
% содержания вещества |
Масса сплава |
Масса меди |
|
1 сплав |
10% = 0,1 |
Х кг |
х * 0,1 |
2 сплав |
25% = 0,25 |
У кг |
у * 0,25 |
сплав |
20 % = 0,2 |
3 кг |
3 * 0,2 |
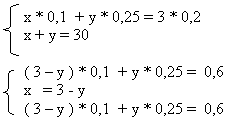
0,15 у = 0,3 у = 2 , значит х = 1.
Ответ: 1 сплав – 1 кг, 2 сплав – 2 кг.
2 способ: ( линейное уравнение)
% содержания вещества |
Масса сплава |
Масса меди |
|
1 сплав |
10% = 0,1 |
Х кг |
х * 0,1 |
2 сплав |
25% = 0,25 |
3 – х кг |
( 3 – х) * 0,25 |
сплав |
20 % = 0,2 |
3 кг |
3 * 0,2 |
х * 0,1 + ( 3 – х ) * 0,25 = 3 * 0,2
х * 0,1 + 0,75 – х * 0,25 = 0,6
– 0,15 х = – 0,15
х = 1, значит 3 – 1 = 2.
Ответ : 1 сплав – 1 кг, 2 сплав – 2 кг.
3 способ: (“крест”)
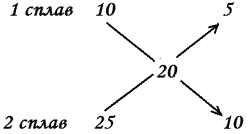
5+10 = 15 частей в 3 кг
3: 15 = 0,2 кг – в 1 части.
На 5 частей – 0,2 * 5 = 1 кг
На 10 частей – 0, 2 * 10 = 2 кг
Ответ: 1 сплав – 1 кг, 2 сплав – 2 кг.
